哈希表
1.简介¶
哈希表是一种数据结构,提供了高效的单点插入与查询操作。
哈希表的本质是利用哈希函数对key进行规模拆分,然后利用各种数据结构如链表、树等结构对哈希冲突的key进行value的存储。
2.哈希函数¶
哈希函数将任意的key作为输入,将key均匀地映射到一个整数值域内。对于大部分情况来说,有:
- key_1= key_2,hash(key_1)= hash(key_2)
-
key_1!= key_2:
-
大部分情况:hash(key_1)!= hash(key_2)
- 小部分情况发生哈希冲突:hash(key_1)=hash(key_2)
由于哈希函数的均匀性,可以看成对于不同的key来说,输出值在输出域内是随机且均匀的。因此,哈希函数在哈希表中的主要作用是规模拆分。
3.哈希表¶
对于随机的输入值,模域上的输出值是概率相等的。
假如我们想要将数据分成等同规模的多份,同时又想要将相同键值的对象聚合到一起,由于哈希函数的特性,就可以根据hash(key)%M进行分区。其中M为分区数,该表达式的输出为分区下标。
因此,哈希表由两部分组成:
- Hash Function
- Hashing Scheme:原意是处理哈希冲突,在分区的目的下可以看成是容纳不同分区数据的数据结构。
哈希表的一个重要的API是查找,通过key寻找唯一的对象。如果希望存放多个key呢?常见的方法是利用容器或者指针存放多个value,或者直接存放多个相同key的对象,但在需要找到所有key对应的对象时需要扫描整个Hashing Scheme。
哈希表的常见实现方式有很多,又分为静态的和动态的。静态哈希表指的表的大小是固定的,动态哈希表则是表的大小随着数据规模的变化而动态增长。
4.静态哈希表¶
4.1.Linear Probe Hashing¶
该方法将哈希表看成一个环形数组。
- Insert:利用哈希函数计算出来该key应该存放的数组下标。若该下标已经有对象了,那么向一个方向顺序扫描,直到找到一个空的位置,将对象进行存储。
- Delete:常见的方法是,在删除的位置添加一个逻辑删除标志。这样在下一次查找的时候,如果遇到该标志则可以继续扫描,若遇到空格则停止。
- Find:与Insert类似。
在最差的情况下,即环形数组已经被填满(存在key或者逻辑删除标志),查找一个不存在的key的复杂度为O(N)。
4.2.Robin Hood Hashing¶
思想是记录对象所在的位置与原本计算出来的位置的偏差值,然后利用偏差值对对象的位置进行调节,尽可能使所有对象的最大偏差值最小。
同样是一个环形数组,插入对象时,若发现空位则直接插入,否则会去不断比对已经占了位置的对象的偏差值。若大于该对象的偏差值,则抢占该对象的位置,并按照同样的方法为这个被抢占的对象找一个新位置。
基于该算法的写入可能会有巨大的代价,这可能会造成对象的连环位移,同时过多的写入可能造成缓存失效,从而进一步降低效率。
4.3.Cuckoo Hashing¶
使用多个hash table,哪个哈希表可以插入就将对象放到哪个哈希表里。大部分情况下,hash table的数量为二。
使用两个哈希函数,可以采用不同的seed,也可以用不同的算法。然后,用一个哈希函数计算第一个哈希表的下标,另一个计算第二个哈希表的下标。
如果其中一个哈希表为空,则选择一个空位置插入;否则选择一个哈希表并将其对象替换掉。
4.4.总结¶
静态哈希表的致命问题是需要提前预估表的大小,这在动态环境中不友好。
但是在用于中间数据结构时拥有不错的性能表现。
5.动态哈希表¶
5.1.Chained Hashing¶
该方法将哈希表看成一个存放各分区的容器的头部,如链表或树,然后将落到该分区的对象存放到该容器中。
若采用链表,该做法的复杂度为O(N/M)。
与其让容器的规模不断增大,我们可以通过增加分区的数量从而将容器控制在一定的规模以下。
5.2.Extendible Hashing¶
对于已经增长到一定规模的容器,我们会将该分区的容器进行拆分,然后获得两个新的分区和概率减半规模的容器。
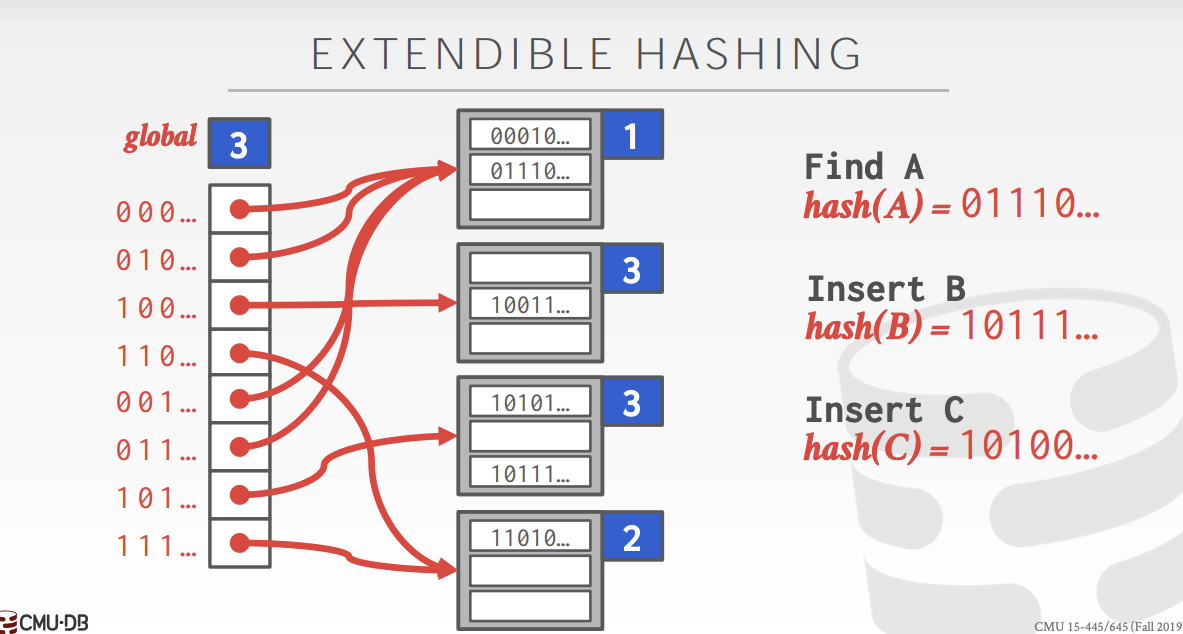
如图,指针表维护一个全局大小global,表示一个数最多需要global位就可以找到它所对应的容器。
容器内部维护一个局部大小local,表示前global位相同的数都共享这个容器。比如图中第一位为0的数都共享local为1的容器,前两位为11的数共享local为2的容器。
当一个容器的大小超过上限时,他首先检查是否需要扩容指针表和global,然后新建两个容器,分别使原来的数加比特位0和加比特位1的数指向这两个新的容器,最后对原来的容器根据规则进行重新分配。
在扩容指针表时,由于需要将表的容量扩为原来的两倍,若global太大,则会造成阻塞的时间过长。
5.3.Linear Hashing¶
维护一个Split Pointer,假设一开始有n个分区,那么同时哈希函数会对两个值进行取模
- hash(key)%n
- hash(key)%2n
该Split Pointer的用处表示Split Pointer以上的分区都是被拆分过的,同时指向下一个即将被拆分的分区。
- 拆分:如果要插入的容器规模大于预设值,则将Split Pointer指向的分区进行拆分,同时Split Pointer指向下一个分区。当Split Pointer指向了第n个分区,那么此时一共有2n个分区。因此,将n变为原来的两倍,删除第一个哈希函数并将指针指向第一个分区。
- 查找:用第一个哈希函数查找到的分区若处于Split Pointer之上,表示该分区已经被拆分过了,应该用第二个哈希函数进行分区查找。
- 删除:进行拆分相反的操作即可。