信息的存储
进制¶
常见的有二进制,十进制和十六进制。书写时可通过下标表示进制,如FF_{16},11111111_2,15_{10},c语言中通过前缀0x或0X表示16进制。
要点:进制间的转换。
字长¶
CPU一次能够并行处理的二进制位数w,也代表了地址的上限2^w-1。
字节序¶
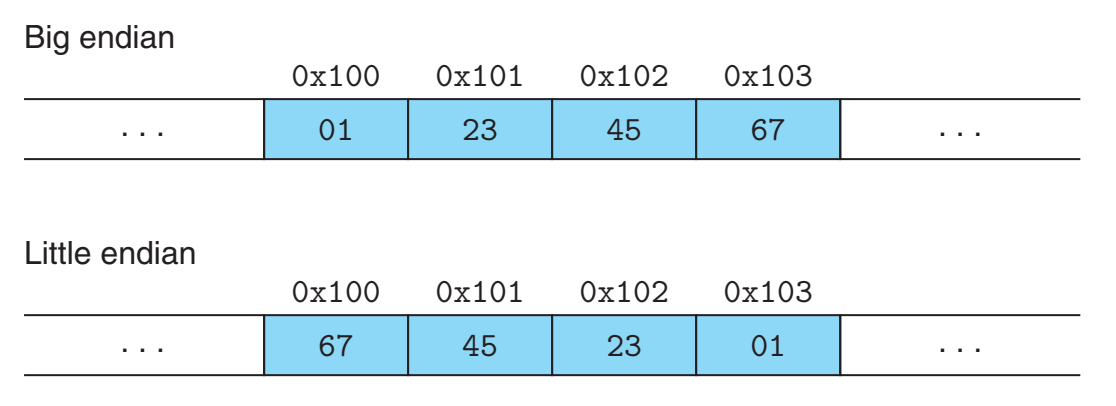
大端序按地址的升序存储字节,而小端序则相反。之所以存在不同的字节序是因为电路优先处理低位字节,因此内部的电路处理都是使用小端序的,而其他场景如网络(网络字节序)或文件存储则使用大端序。
整数¶
c语言中的整数有很多,区别主要在位数和有无符号,有符号整数的最高一位是符号位,和其他位是正数相反,符号位表示的是负数。
有符号整数的值为w=-x_{i-1}2^{w-1}+\sum^{w-2}_{i=0}x_i2^i,w\in[-x_{i-1}2^{w-1},2^{w-1}-1],其中w为位数。
有符号整数的值为\sum^{w-1}_{i=0}x_i2^i,w\in[0,2^w-1],其中w为位数。
整数需要注意的主要是溢出以及有符号和无符号整数之间运算可能产生的问题。
浮点数¶
最开始浮点数的实现百花齐放,产生了许多由协议不一致导致的问题。最后定下了IEEE标准,也就是今天绝大多数浮点数的实现协议。
假设浮点数的整数有n位,小数有m位,则浮点数的表示为w=\sum^m_{i=-n}x_i2^i。
可以发现,浮点数只能通过若干二的幂次分之一\frac{1}{2^x}的分数不断逼近小数,因此很多时候是无法精确的表达一个小数的,即精度丢失。
同时,在浮点数总位数固定的情况下,精度越高,即小数部分的位数m分配的越多,那么整数部分的位数n则分配的越少,值域越低,反之亦然。
IEEE的标准下,浮点数由三部分组成
- 符号位s
- 指数域,由k位组成,指数E=\sum^{k-1}_{i=0}e_i2^i-Bias,Bias=2^{k-1}-1
- 分数域,由n位组成, 标准表达式下分数M=1+\sum^{n-1}_{i=0}f_i2^{-i},非标准表达式下M=\sum^{n-1}_{i=0}f_i2^{-i}
则浮点数w=(-1)^sEM 。

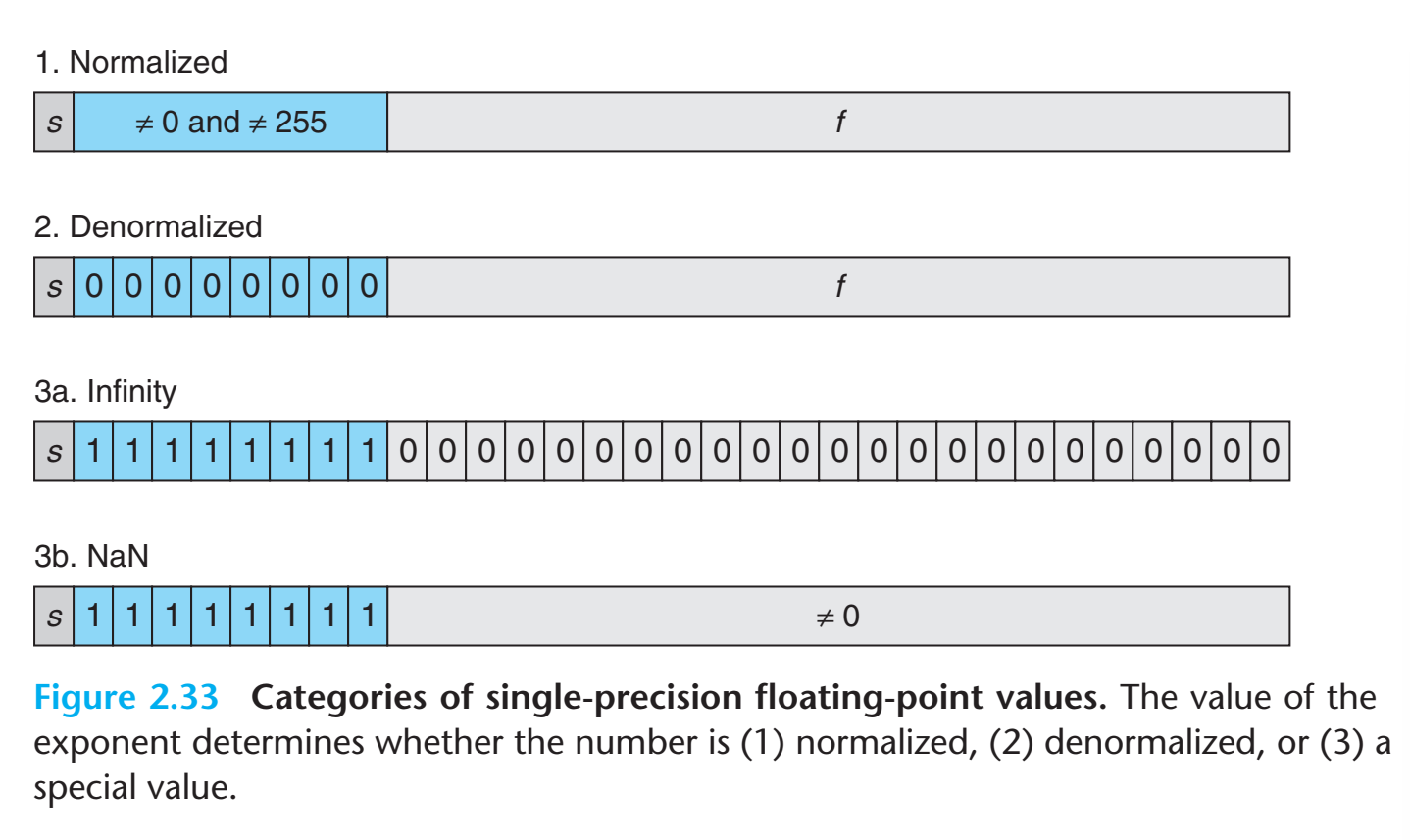
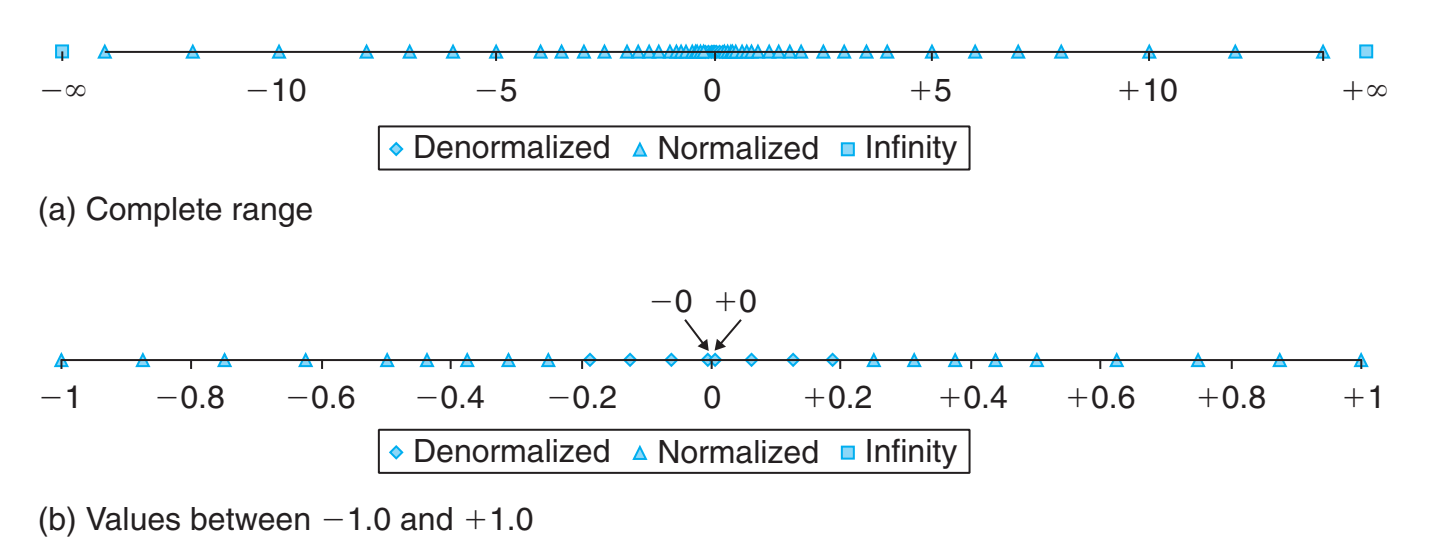
标准表达式中为了获取额外的一个位数隐含约定了1的偏移量,这也导致了无法表达一个无限接近于0的数,因此设计非标准表达式解决这个问题。
同时,指数域为了方便两个数进行大小比较,也隐含约定了偏移量,从而利用了无符号整数的优点,也可以使用有符号整数的负数值域。
以及两个特殊的表达形式,无限大和NaN(not a number),用于表达溢出和不合法的数。